Christian Weilbach and Will Harvey, under the supervision of Dr. Frank Wood (PLAI group), have just released a paper on a new deep generative framework to learn structured diffusion models. In contrast to our approach, picture a traditional algorithm design that requires careful mathematical reasoning and a precise implementation in light of numerical and/or combinatorial knowledge. Our new framework instead leverages the universal framework of amortized inference to learn an approximate algorithm while gradually allowing incorporation of such knowledge as side information. Traditional amortized inference uses only joint examples of inputs and outputs. While this sometimes can work on our problems, we have found the incorporation of structural knowledge of computation to be very beneficial both in terms of sample efficiency and ability to generalize on problem size. The following figure provides a high-level overview of our framework,
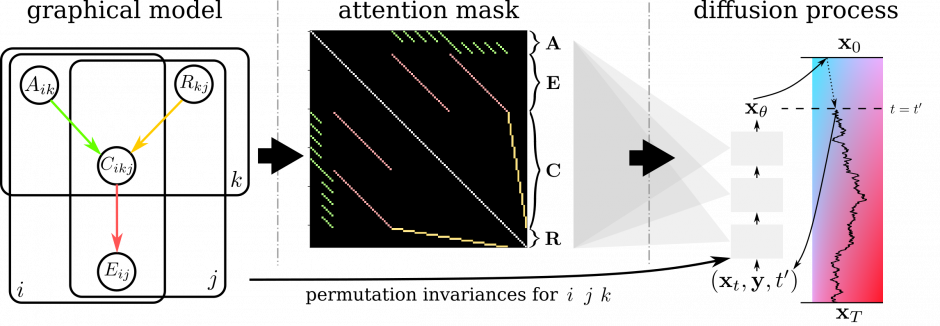
In the first panel the computational graph of the multiplication of the continuous matrix A and the binary matrix R is expanded as a probabilistic graphical model in which intermediate products C are summed to give E = AR. This graph is used to create a structured attention mask M, in which we highlight 1’s with the color of the corresponding graphical model edge and self-edges in white. In the third panel the projection into the sparsely-structured neural network guiding the diffusion process is illustrated. In the bottom the translation of permutation invariances of the probability distribution into the embeddings is shown. You can find the details of our method in Section 3 of the paper.
Let’s take a look at the resulting dynamics trained to solve Sudokus, to perform binary continuous matrix factorization and to sort. Here you can see our Sudoku solver (trained without access to any existing solver):
If you have solved Sudokus you know that you need to satisfy the constraints that each row, each column and each 3×3 block must contain all numbers from 1 to 9. We have visualized violations of these constraints in red for each row, column and block. On a first glance at the video you can see that the red is gradually being reduced from beginning to the end of the process until both Sudokus are solved. If you take a closer look you can see which parts of the Sudoku are solved first and which parts superimpose the most constraints (are most red). Compared to common solution strategies our solver inherits the stochastic nature of the underlying denoising diffusion process, which yields a more gradual trial and error behaviour than deterministic solvers, but nonetheless steadily moves towards the solution. This also means that the algorithm provides sample diversity as can be seen in our paper (Figure 8). Given several restarts our algorithm solved all 100 Sudokus with that we tested on, each of which had 16 clues given.
We also trained an algorithm for varying rank binary matrix factorization, i.e. the factorization of a matrix E into a binary matrix R and a continuous matrix A. In the video you can see the solution of a problem instance of rank 3 factorization for 5 continuous dimensions and 10 binary dimensions. The process again starts with a noisy solution and gradually refines it into the right binary structure to select the proper rows of A for each row of E. The binary structure converges quicker, while the values of A are still refined until the end of the algorithm execution.
To cover a different class of algorithmic problems we also trained a sorting algorithm. Here you can see it sorting a list of 30 elements.
By incorporating both combinatorially hard and mixed continuous discrete problems and being able to address problems of varying dimensionality we are able to cover a wide range of algorithmic problems while putting a lot less additional work on the designer of our amortized inference artifacts. Thanks for taking the time to read this and I hope you got curious and check out the details in the paper.